a kerület meghatározása
A kerület az egyik legegyszerűbb és alapvető geometriai ábra, amelyről tudunk. Meghatározhatnánk egy kört, mint egy zárt görbe vagy kerület által generált ábrát, amelyben nincsenek csúcsok vagy belső szögek. Ezenkívül a kerületnek nincsenek megkülönböztetett oldalai, mint más ábráknál, például a négyzetnél vagy a háromszögnél.
A kerület meghatározásához kezdhetünk azzal, hogy odafigyelünk a szó etimológiai jelentésére, ami latinul azt jelenti, hogy „cipelni”. A kerület általában összekeverhető a kör, de ha helyesen beszélünk, azt kell mondanunk, hogy ez egy kör belső felülete, míg ez a kerülete.
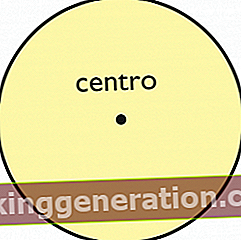
A kerület mindig kétdimenziós és sugara van, amely a talált pontok (amelyek az ábra határát jelzik) és a középpont közötti távolságot jelentik. Ezenkívül a kerületet alkotó egyéb elemek a középpont (az ábra többi pontjától egyenlő távolságra lévő pont), az átmérő (a középponton áthaladó két legtávolabbi pont közötti távolság), az akkord (bármely szakasz, amely a kerület egyik két pontja), a szekundáns és az tangens vonalak (az első az, amelyik áthalad az ábra belsején és kívül, két szektorra osztva; a második az a vonal, amely kívülről halad és megérinti a kerületet csak pont).
Ami a kör szögeit illeti, ezek lehetnek központi, feliratos, félig beírt, belső és külső. Ezenkívül két vagy több kör jelenlétében különböző kapcsolatok is létrejöhetnek. Itt kell beszélnünk a külső kerületekről (azokról, amelyek nem osztoznak közös pontokon), a külső vagy belső érintőkről (azokról, amelyeknek csak egy közös pontja van, kívülről vagy belül egy közös pont), a szekundákról (amelyek két részre oszlanak) szegmensek mindegyikét a metszéspontok által generált mindkettő), az excentrikus és a koncentrikus belső terek (függetlenül attól, hogy ugyanazzal a középponttal rendelkeznek-e). Végül az egybeeső körök azok, amelyeknek középpontja és sugara azonos, és amelyek egyetlen ábrán konvergálnak.
