a trigonometrikus azonosságok meghatározása
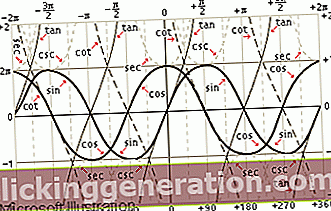A trigonometrikus azonosságok fogalma egy olyan fogalom, amelyet a matematika területén a geometriai ábrán található változó trigonometrikus függvényekre utalnak. A trigonometria a matematika azon ága, amely a háromszögek elemzésére és tanulmányozására szakosodott, különös tekintettel az esetlegesen létező különféle szögek alakjaira, jelentéseire és értékeire. A trigonometrikus azonosságok ekkor azoknak az értékeknek az eredményei lesznek, amelyek változóak és nagyon változatosak.
A matematika számos eleméhez hasonlóan az ősi idők óta léteznek olyan fogalmak, amelyekben a görög filozófusok már meghatározták a geometriai alakzatok szögeinek függvény- és értékfogalmait. Ezeket a fogalmakat csak a modernitás javítaná, a XVII. Században, amikor algebrai szempontból megjegyezték, hogy mindenféle számítást képesek elvégezni a különböző szögek között.
A trigonometrikus azonosságok tágan definiálhatók, mint minden lehetséges szögváltozó, amely létezhet egy geometriai ábrán. Ezeket az azonosságokat mindig a görög betűk képviselik, például alfa, béta, omega stb. Az egyes identitások változóinak meghatározásához olyan elemeket is használnak, mint a Celsius-fok. A legismertebbek azok, amelyek a szinusz és a koszinusz, a szinusz és az érintő között jönnek létre stb. A trigonometrikus azonosságok egyszerűsített formák, amelyek lehetővé teszik számunkra a trigonometria különböző funkcióinak végrehajtását és megismerését. A matematika ezen kérdései, pontosabban a trigonometria arra szolgálnak, hogy megszervezzék azokat a különböző számításokat, amelyeket az egyes adattípusok specifikus függvényeiből kell elvégezni. A trigonometrikus azonosságok nagymértékben változóak, és lehetővé teszik az egyes trigonometrikus függvények (azaz az értékek) különböző esetekhez való különféle és különböző módon való ábrázolásának lehetőségét.
