algebra meghatározása
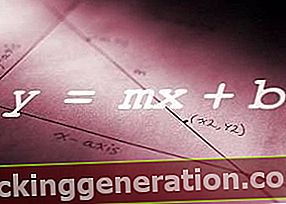Az algebra a matematika azon területe, amely felelős a struktúrák, összefüggések és mennyiségek vizsgálatáért. Az algebrában és ellentétben a számokat használó aritmetikával ezeket szimbólumokkal helyettesítik, több okból is, először is azért, mert könnyebb megfogalmazni az általános számtani törvényeket, például a + b = b + a, másodszor, mert lehetővé teszi ismeretlen számokra való hivatkozást, egyenletek megfogalmazását és azok megoldásának tanulmányozását, végül pedig azért, mert a szimbólumok funkcionálisabbak a funkcionális kapcsolatok megfogalmazásakor, bocsásson meg a redundanciát.
Másrészt az algebrai struktúrák olyan elemek összessége, amelyek bizonyos működési tulajdonságokkal rendelkeznek, míg a struktúrát azok a műveletek határozzák meg, amelyek elvégezhetők az említett halmazt alkotó elemekkel, és azok a matematikai tulajdonságok, amelyeket ezek a műveletek magukban foglalnak. A leggyakoribb algebrai struktúrák közül megemlíthetjük: többek között a csoportot, gyűrűt, testet, monoidot, vektorteret, modult.
Ahogy fentebb mondtuk, az algebra különféle jeleket és szimbólumokat használ amelynek természetesen az algebrai kontextusban lesz egy bizonyos jelentése. Például a + jel az összeadást fejezi ki, és bináris műveletek kifejezésére szolgál, az ábécé első betűi az ismert mennyiségek kifejezésére, míg az utolsó betűk éppen ellenkezőleg, az ismeretlenekre utalnak, az n betű ismert. akkor használható, ha tetszőleges mennyiséget és co-t akar kifejezni, hogy többek között állandó kifejezésekre utaljon.
